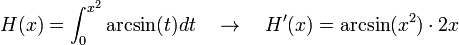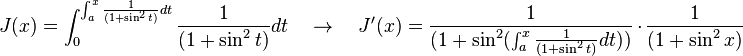Popular Posts
-
Integral de una constaste por una función de x Integración Integrar es el proceso recíproco del de derivar , es decir, ...
-
Operaciones con matrices (suma, diferencia, multiplicación) Dar a conocer lo aprendido en la clase del tema "operaciones con mat...
-
Derivadas parciales. Objetivo: Dar a conoser lo aprendido en la clase del tema “Derivadas parciales Una derivada pa...
-
Regla Cramer Dar a conocer lo aprendido en la clase del tema "Regla cramer" La regla de Cramer es un teorema del álge...
-
Reducción de gauss y Gauss- Jordan Dar a conocer lo aprendido en la clase del tema "Reducción de gauss y Gauss- Jordan" ...
-
Sistemas de ecuaciones lineales consistentes, inconsistente y su representación para métrica del conjunto solución Dar a conocer lo ...
-
Integral definida Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica ...
-
Expansión de cofactores Dar a conocer lo aprendido en la clase del tema "Expansión de cofactores" ...
-
Métodos para resolución de sistemas de ecuaciones lineales: Método gráfico, igualación, sustitución, eliminación (sumas y 10) Dar a...
Con tecnología de Blogger.
Blog Archive
-
▼
2014
(47)
-
▼
noviembre
(47)
- 2.3.7 Regla de la potencia
- 2.3.7.2 Integrales que incluyen funciones funcione...
- 2.3.4 integral de en
- 4.3.4 Regla cramer
- 4.3.3 propiedades de los determinantes
- 4.3.2 Expansión de cofactores
- 4.3.1 Definición de una determinante
- 4.2.4 matriz inversa
- 4.2.3 Propiedades de las operaciones matrices
- 4.2.2 operaciones con matrices (suma, diferencia, ...
- 4.2.1 Tipos de matrices cuadradas, rectangulares, ...
- 4.2 Álgebra de matrices
- 4.1.5.5 Sistemas homogéneos
- 4.1.5.4 Reducción de gauss y Gauss- Jordan
- 4.1.5.3 Operaciones elementales sobre renglones
- 4.1.5.2 Expresión matricial de un sistema de ecuac...
- 4.1.5.1 Definición de Matriz
- 4.1.5 Eliminación de Gauss y Gaus - Jordan
- 4.1.4 Sistemas de ecuaciones equivalentes
- 4.1.3 Métodos para resolución de sistemas de ecuac...
- 4.1.2 sistemas de ecuaciones lineales consistentes...
- 4.1.1 Definición
- Modulo 4. sistemas de ecuaciones lineal y matrices
- 3.3 Propiedades de la integral definida
- 3.2 Teorema fundamental del calculo
- 3.1 área bajo la curva
- 3.4 Área entre 1 y 2 curvas.
- Modulo 3 Integral definida
- 2.3.11 integrales por partes
- 2.3.10 integrales que incluyen au
- 2.3.9 integrales que las (1/u) a u
- 2.3.8 integrales que incluyen funciones logarítmicas
- 2.3.7.1 Integrales que incluyen u(n)
- 2.3.6 integral de una suma (diferencia) de funciones
- 2.3.5 integral de una constaste por una función de x
- 2.3.3 Integral xn
- 2.3.2 Integral de una constante por una variable
- 2.3.1 Integral indefinida de una constante
- 2.3 Formulas básicas de integración
- 2.2.1 Integración con condiciones iniciales
- 2.2 integral definida
- 2.1 Antiderivada
- Modulo 2 Integración
- 1.3 Máximos y mínimos de funciones de 2 variables.
- 1.2 Derivadas parciales.
- 1.1 Funciones en dos variables
- Objetivo General
-
▼
noviembre
(47)
Acerca de mí
Blogroll
Archivo del Blog
-
▼
2014
(47)
-
▼
noviembre
(47)
- 2.3.7 Regla de la potencia
- 2.3.7.2 Integrales que incluyen funciones funcione...
- 2.3.4 integral de en
- 4.3.4 Regla cramer
- 4.3.3 propiedades de los determinantes
- 4.3.2 Expansión de cofactores
- 4.3.1 Definición de una determinante
- 4.2.4 matriz inversa
- 4.2.3 Propiedades de las operaciones matrices
- 4.2.2 operaciones con matrices (suma, diferencia, ...
- 4.2.1 Tipos de matrices cuadradas, rectangulares, ...
- 4.2 Álgebra de matrices
- 4.1.5.5 Sistemas homogéneos
- 4.1.5.4 Reducción de gauss y Gauss- Jordan
- 4.1.5.3 Operaciones elementales sobre renglones
- 4.1.5.2 Expresión matricial de un sistema de ecuac...
- 4.1.5.1 Definición de Matriz
- 4.1.5 Eliminación de Gauss y Gaus - Jordan
- 4.1.4 Sistemas de ecuaciones equivalentes
- 4.1.3 Métodos para resolución de sistemas de ecuac...
- 4.1.2 sistemas de ecuaciones lineales consistentes...
- 4.1.1 Definición
- Modulo 4. sistemas de ecuaciones lineal y matrices
- 3.3 Propiedades de la integral definida
- 3.2 Teorema fundamental del calculo
- 3.1 área bajo la curva
- 3.4 Área entre 1 y 2 curvas.
- Modulo 3 Integral definida
- 2.3.11 integrales por partes
- 2.3.10 integrales que incluyen au
- 2.3.9 integrales que las (1/u) a u
- 2.3.8 integrales que incluyen funciones logarítmicas
- 2.3.7.1 Integrales que incluyen u(n)
- 2.3.6 integral de una suma (diferencia) de funciones
- 2.3.5 integral de una constaste por una función de x
- 2.3.3 Integral xn
- 2.3.2 Integral de una constante por una variable
- 2.3.1 Integral indefinida de una constante
- 2.3 Formulas básicas de integración
- 2.2.1 Integración con condiciones iniciales
- 2.2 integral definida
- 2.1 Antiderivada
- Modulo 2 Integración
- 1.3 Máximos y mínimos de funciones de 2 variables.
- 1.2 Derivadas parciales.
- 1.1 Funciones en dos variables
- Objetivo General
-
▼
noviembre
(47)
- Home »
- 3.2 Teorema fundamental del calculo
jason
On lunes, 24 de noviembre de 2014
Teorema fundamental del calculo
Dar a conocer lo aprendido en la clase
del tema "Teorema fundamental del calculo "
El teorema fundamental del cálculo consiste (intuitivamente) en la afirmación de que la derivación e integración de una función
son operaciones inversas. Esto significa que toda función continua
integrable verifica que la derivada de su integral es igual a ella
misma. Este teorema es central en la rama de las matemáticas denominada análisis matemático o cálculo.
Primer teorema fundamental del cálculo
Dada una función f integrable sobre el intervalo |
Demostración
Lema
Sea integrable sobre
integrable sobre ![[a,b]](http://upload.wikimedia.org/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) y
yDemostración del lema
Está claro que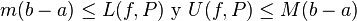 para toda partición
para toda partición  . Puesto que
. Puesto que  , la desigualdad se sigue inmediatamente.
, la desigualdad se sigue inmediatamente.Demostración
Por definición se tiene que .
.Sea h>0. Entonces
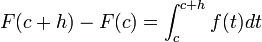 .
.Se define
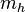 y
y 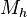 como:
como:-
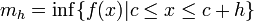 ,
,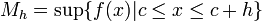
-
 .
.
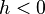 . Sean
. Sean-
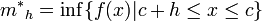 ,
,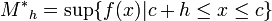 .
.
-
 .
.
-
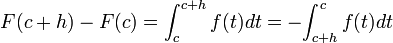 ,
,
-
 .
.
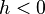 , se tiene que
, se tiene que-
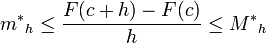 .
.
 es continua en c se tiene que
es continua en c se tiene que-
 ,
,
-
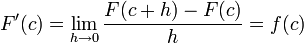 .
.


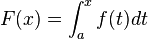 . Si f es
. Si f es  , entonces F es
, entonces F es  y F'(c) = f(c).
y F'(c) = f(c).
![m \leq f(x) \leq M \; \forall x \in [a,b]](http://upload.wikimedia.org/math/1/e/1/1e1b2ad811ce2c15f191c634ded2afd9.png)